Порядковая нумерация
Текст книги Ле Корбюзье «Модулор-2» ("Le Modulor II", Le Corbusier, 1955) публикуется по изданию «Модулор. MOD 1. MOD 2». Перевод с французского Ж.С. Розенбаума. Стройиздат. 1976.
«Это система пропорций, мешающая делать плохо и помогающая делать хорошо».
Эйнштейн. Принстон, 1946г.
В 1949 году газета «Франс-Суар» напечатала под рубрикой «За четверть часа вы узнаете все:.. Архитектор Ле Корбюзье ополчился против метра... Долой метрическую систему! .. далее, ряд положений подтверждали это заявление. Но это же журналистика! Она способна даже с лучшими намерениями поднять шум, часто просто невыносимый. Она идет на скандал! Я никогда и не помышлял об уничтожении метрической системы (читай «Модулор», 1948). Метрическая система — это средство для измерения, основанное на десятичной системе; именно это обстоятельство превратило ее в современный рабочий инструмент.
До сих пор размерные величины шкалы Модулора выражались как в метрической (десятичной) системе мер, так и в футах-дюймах (в системе не десятичной). Это помогает тем, кто пользуется футами и дюймами, производить все подсчеты и расчеты в десятичной системе.
В статье, опубликованной в журнале «Cahiers du Sud», Андре Воженский отметил ряд неточностей принятой в «Модулоре» 1948 года терминологии, в частности, в заглавии «Опыт всеобщей гармоничной системы мер»... Думаю, что было бы правильным озаглавить: «Опыт гармоничной системы мер в человеческом масштабе, имеющей всеобщее применение и т. д...» Этот вопрос так и остался открытым. Он отмечает, что величины интервалов между делениями Модулора, стремящихся с одной стороны к пулю, а с другой к бесконечности, не пронумерованы путем применения простых порядковых чисел как для микроскопически малых, так и для астрономических по величине интервалов... Полагаю, что это ни для кого не было связано с серьезными осложнениями и никому не служило помехой. Во всяком случае, с чисто теоретической точки зрения можно утверждать, что пропорциональная шкала Модулора представляет собой как бы лестницу размерных величин, не опертую на что-либо, поскольку эти величины никогда не достигают нуля. С другой стороны, она не подвешена к некоему гипотетическому небу, так как стремится к бесконечности. Это все чистая софистика! Он, однако, имел полное право приводить цитаты. Если мы хотим установить порядковую нумерацию для Модулора, следует начинать с какой-либо реальной величины, приняв ее за первую порядковую величину (цифра «1»). От этой точки можно будет идти вверх и вниз. Найти такую начальную величину не так просто. Лица, к которым я обращался с этим вопросом, не удостаивали меня ответом, а иногда высказывали мысль, что этот вопрос не представляет интереса. Правда, одна из опрошенных легкомысленно сказала: «Считайте начальной точкой подошву стопы стоящего человека». В графической эмблеме Модулора ноги, действительно, на земле; человек встал на землю, иначе говоря, опустился на нулевую отметку. Мы, однако, неоднократно указали, что нуль — это недосягаемая цель. Он показывает только общую тенденцию: однако сам недосягаем. В июне 1951 г. я предложил Крюссару принять начальную точку нумерации в соответствии с рис. 67. Эта точка находится на отметке 113; тогда нижние деления по направлению к нулю были бы обозначены порядковыми номерами 1, 2, 3, 4, ..., 20, ..., 100, ..., 200 с индексом хотя бы А. Они имели бы начертания 1А, 2А, ЗА, 4А, 100А, 200А и быстро бы достигли обозначения микроскопических размеров.
Порядковые номера делений выше отметки 113 получили бы индекс В; нумерация делений не имела бы пределов — 1, 2, 3, 4, 5, 9, 27, 99, 205 и т. д. и имела бы начертания 1В, 2В, 3В, 4В, 5В, 9В, 27В, 99В, 205В и т. д.
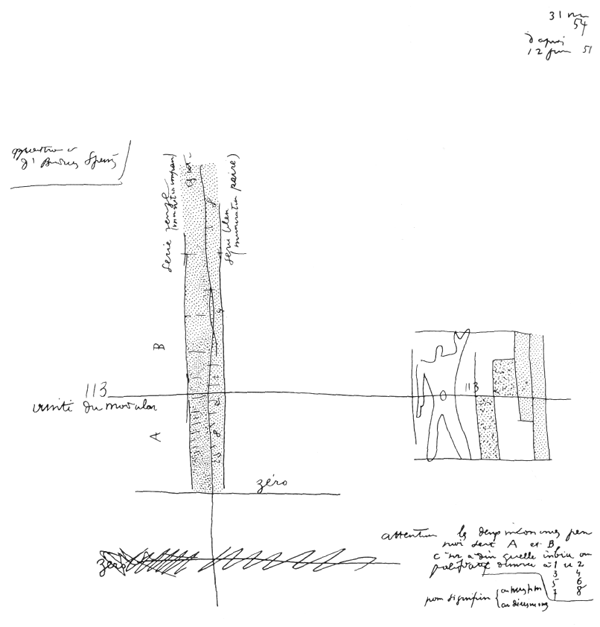
Подобный метод порядковой нумерации представляется мне отвратительным, он лишен всякой выразительности, он бесцветен. Я предоставил ученым возможность определить четкую и удобную систему. Я подчеркиваю: и удобную, так как на основе этой нумерации будут проводиться вычисления: сложение, вычитание, умножение, деление и т. д., быть может, придется даже составлять алгебраические уравнения. В этих случаях, как мне кажется, индексы А и В создадут ряд неудобств; тем не менее, на мой взгляд, надо придумать индексы, которые отмечали бы «нижние» и «верхние» числа в рядах.
Отметка 113 отмечает наиболее существенную точку Модулора: она отвечает половине размерной величины 226 (синий ряд) и проходит через солнечное сплетение человека с поднятой рукой и т. д., и соответствует членению в золотом отношении величины 183, т. е. роста стоящего человека (красный ряд). Вопрос о порядковой нумерации Модулора остается открытым. Может быть, ответ на этот вопрос подскажут читатели?...



Добавить комментарий