Доказательства. Дискуссия
Текст книги Ле Корбюзье «Модулор-2» ("Le Modulor II", Le Corbusier, 1955) публикуется по изданию «Модулор. MOD 1. MOD 2». Перевод с французского Ж.С. Розенбаума. Стройиздат. 1976.
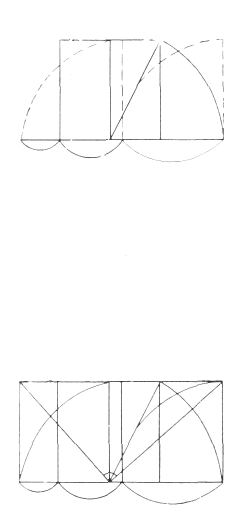
Вот окончательная схема Модулора (рис. 3). Два равных квадрата со сторонами ИЗ см поставлены один на другой. Третий квадрат наложен на них с отношением частей, отвечающих золотому сечению; его положение определено правилом вписанного прямого угла.
Прямой угол строго (на этот раз) вписан в прямоугольник, состоящий из двух квадратов, и определяет две точки в местах пересечения сторон третьего квадрата...
Проведя наклонную прямую через эти две точки, мы получаем слева убывающий ряд, а справа возрастающий, определяющие замечательную спираль синих и красных рядов пропорциональных чисел. В мае 1950 года Дюфо де Кодеран из Жиронды обратил мое внимание на ошибку, допущенную в первой книге «Модулор-1».
 |
 |
 |
«Вам, конечно, понятна радость, охватившая меня при мысли, что со временем система Модулора получит массовое распространение и даст нам возможность любоваться безграничным великолепием пропорциональных отношений. Можно сказать в конечном итоге, что это изумительно...» Наряду с этим он указывает на ошибку: «...эта ошибка может поколебать доверие к всеми признанной системе; к счастью, это относится только к теоретической части и не помешает практическому внедрению Модулора.
Речь идет о графическом изображении рядов Модулора, в которое, по моему скромному мнению, вкралось множество ошибок, а в отдельных случаях и неопределенностей, препятствующих нахождению правильного решения.
Я предлагаю иное, весьма простое построение, лишенное этих недостатков и способное удовлетворить любого придирчивого критика (существуют, конечно, и другие построения, способные привести к аналогичному результату).
 |
 |
 |
Итак, разрешите без лишних слов перейти к изложению своих замечаний:
Вписать прямой угол, о котором идет речь, в два квадрата невозможно. Если это действительно два квадрата, то угол не прямой. Если угол прямой, то один из двух четырехугольников не является квадратом.
Положение вписанного прямого угла может быть определено полуокружностью, построенной на прямой, равной удвоенной стороне квадрата. Это единственное решение.
Ниже я позволю себе изложить предлагаемое решение:
Исходный квадрат / Его золотое сечение
Двойной квадрат построен с помощью красной точки, положение которой определено золотым сечением». Предложение мсье Дюфо важное, точное, весьма простое и изящное. Но ... ведь я-то шел другим путем! Мой ответ был следующим:
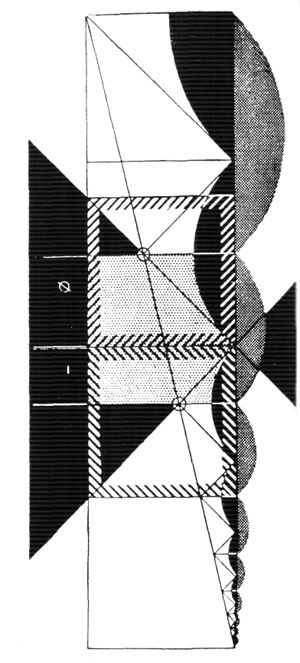
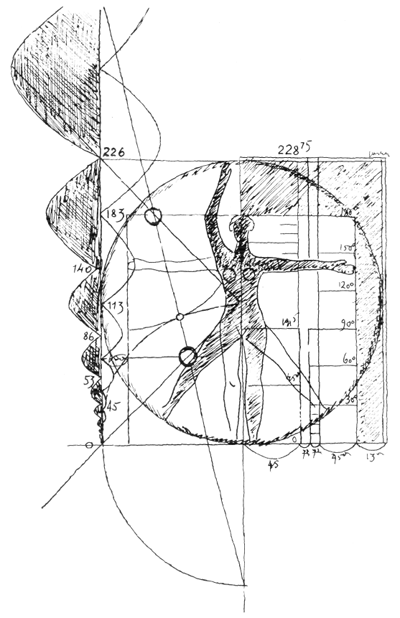
«На чертеже А — я воспроизвел ваше построение. На чертеже В — я привожу свое построение, (см. «Модулор-1», рис. 14). Исходные данные были положены в основу пропорциональной сетки: Человек с поднятой рукой = 2 квадрата со сторонами 113 (226).
Положение третьего квадрата определено «правилом вписанного прямого угла».
Положение третьего квадрата должно было бы быть определено делением стороны этого квадрата в отношении золотого сечения, а не делением пополам. Отсюда и отмеченная ошибка (в «Модулоре», 1948 г.) в рис. 3, 4, 5, 6, 9, приводящая к неясностям и неопределенностям в рис. 18 и 60.
Такое предположение (рис. 2) является результатом естественной игры воображения. То было предварительным априорным представлением, а не результатом расчета.
Так было определено положение точки i (рис. 6, Mod-1). Это повторяется (рис. 9) при определении положения точки l длины и прямой g — 1, на которой путем деления на равные части построены два равновеликих квадрата с основаниями gk и ki. Я согласен, мсье Дюфо, что в этом построении стремились выразить определенную идею и не ставилась задача обеспечить полную точность чертежа. Построение Дюфо весьма четкое и простое, но выполненное апостериори, и не могло бы кому-либо прийти в голову: это, по существу, построение проверочное и уточняющее».
Сейчас (в 1954 году) надо учитывать условия, в которых проводилась работа тогда (1942—1948 годы). Мы пытались создать пропорциональную сетку, рабочий инструмент для строительных площадок. Мы подошли к определению взаимосогласованных чисел.
Мы ставили себе практическую цель: оказать помощь строительной площадке. В те годы мы строили жилой дом в Марселе (Жилую единицу).
•
Жюстен Серральта и Мезонье стремились выяснить возможность согласования Модулора с традиционными системами прошлого, в частности с египетских локтем.
Меня поразило, что Модулор впервые обеспечил гармоничную соразмерность — пропорциональность, основанную па размерах человеческой фигуры. Это поистине любопытно. В эпоху Возрождения с увлечением занимались вопросами пропорций («божественные пропорции»). Тогда упивались математическими выкладками, использованием чисел во всяких алгебраических и геометрических построениях. Строились великолепные многогранники с вписанными них осевыми линиями и окружностями, в которые в свою очередь вписывались фигуры человека и плащи сооружений.
Безграничная игра цифровых сочетаний позволяла в каждом отдельном случае создавать свою систему размеров. Система «божественных пропорций» в одинаковой мере подчиняла себе построение как здание высотой до 100 метров, так и гончарные изделия в несколько сантиметров. В ту пору чрезмерно увлекались самим рисунком пропорциональных построений, придавая им самодовлеющее значение. Рисуя многочисленные многогранники и звездообразно расходящиеся оси, часто забывали, что глаза у человека расположены на лицевой стороне головы и что в зависимости от его роста меняется зрительное восприятие предметов. Так утрачивалось понимание истинного взаимоотношения между человеком и окружающей его средой.
Человек уже на заре своего развития создал приспособления, оказывающие ему практическую помощь и, что еще важней, доставляющие ему моральное удовлетворение.
Он изобрел средства измерения, имя которых: фут (стопа), локоть, пядь, дюйм, сажень и т. д., и т. д.... Используя эти орудия (измерения), он строил дома, дороги, мосты, дворцы и соборы. Эти меры: фут (стопа), пядь, локоть и т. д.... происходят от частей человеческой фигуры. Они способствуют созданию гармонических отношений и подчиняются так же математическим закономерностям роста и развития, как и живые существа.
Парфенон, пирамиды, храмы, дома рыбаков и хижины пастухов построены на основе этих присущих человеку размеров.
Впоследствии была принята метрическая система исчисления; это было грандиозным изобретением. Всякие расчеты при применении системы футов и дюймов крайне сложны и трудоемки. Однако размерные величины в 10, 20, 30, 40, 50 сантиметров или в 1, 2, 3, 4, 5 метров никак не связаны с размерами нашего тела. Неожиданно для самого изобретателя Модулор дал возможность создавать широкое разнообразие математических и геометрических сочетаний, которые могут быть выражены как в метрах, так и футах-дюймах и т. д. ... Все назначенные по Модулору размеры основаны на размерах нашей фигуры и поэтому позволяют создавать предметы, приспособленные к человеку и его окружению, в области как архитектуры, так и механики.
Вся гамма числовых размеров Модулора с одной стороны стремится к нулю, а с другой устремляется в бесконечность; в пределах человеческого роста, т. е. от 0 до 2 м 26 см, она делится на небольшое и, возможно, слишком ограниченное число интервалов; не исключено, однако, что эта ограниченность является ее достоинством!
Кое-кто исследовал связь между старыми системами мер и Модулором. Были установлены поразительные совпадения. Исследование Серральта и Мезонье позволило включить общие для обеих систем мер промежуточные величины, заимствованные у системы египетского локтя.
Египетский локоть широко применялся в античные времена. Возможно, что он обогатит ряды размерных чисел Модулора, которые можно будет тогда сочетать со старыми мерами: дюймом, пальмой, футом и локтем.
В пальме — четыре дюйма,
в футе — четыре пальмы,
в локте — один фут и две пальмы.
Древние цивилизации зарождались в определенных географических районах и в разных общественных формациях. Разными были и единицы меры. Так, египетский локоть равен 45 см, греческий — 46,3 см, римский — 44,4 см. При возведении культовых сооружений в древнем Египте применялся более крупный, царский локоть, равный 52,5 см, что сообщало обителям богов подчеркнуто величественные масштабы. В Марокко применяется локоть длиной 51,7 см и иногда 53,3 см, в то время как размер тунисского локтя снижен до 47,3 см, а в Калькутте — до 44,7 см и в Цейлоне — до 47 см. В арабских странах применяли так называемый локоть Омара, равный 64 см. Римская пальма равнялась 1/4 фута, т. е. 7,4 см, и именовалась «Пальма-минор»; другая, так называемая «пальма-мажор», равнялась 3Д фута. Эти единицы измерения применялись вплоть до появления метрической системы, причем в разных местах они имели различные значения: в Карраре основной единицей измерения был фут, равный 24,36 см, в Генуе — 24,7 см, в Неаполе — 26,3 см, в Риме — 22,3 см и т. д.
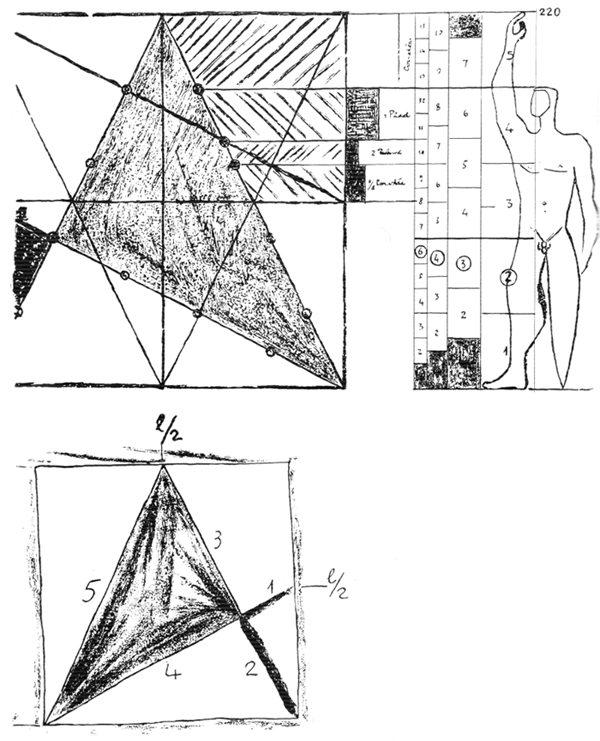
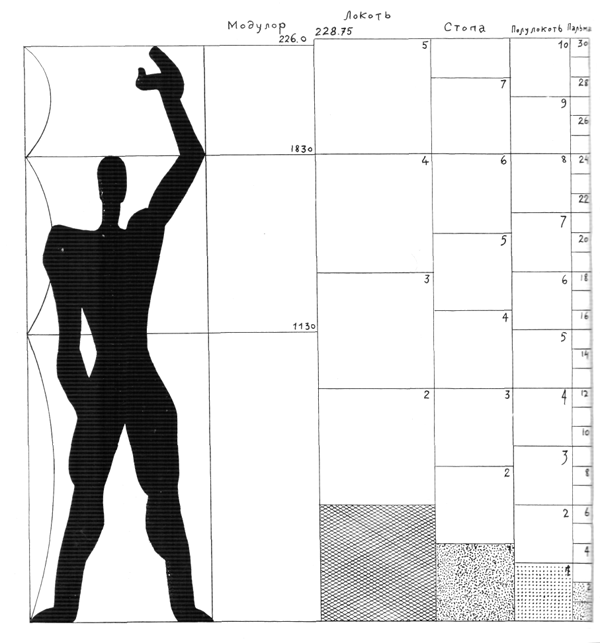
На рис. 5, выполненном Серральта и Мезонье, принят за основу квадрат с вписанной «фигурой человека ростом 1,83». Но Серральта, как человек с нежным сердцем, вместо мужчины изобразил женщину ростом (о ужас!) 1 м 83 см. В два поставленные друг па друга квадрата со сторонами 113 + 113 = 226, вписан прямой угол, точки пересечения которого служат основой построения... Высота 183 равна четырем локтям по 45,75 см или шести футам по 30,5 см, а каждый фут — четырем пальмам по 7,625 ...
Отмечается лишь одно расхождение в отметках по Модулору на основе (183) — 226 и на основе египетского локтя (183) — 228,75. Ниже мы увидим, что подобные расхождения, которые можно назвать «доборами», не создают существенных неудобств в строительном деле, когда они относятся к дополнительным элементам. Выражение Модулора в египетских локтях согласует Модулор с древними геометрическими построениями. На рис. 4 величины 1, 2, 3, 4 и 5 получены исходя из квадрата, в который вписан треугольник путем деления сторон квадрата пополам.
На рис. 6 это же построение приведено в более упорядоченном, выразительном и четком виде. Показано членение размера 228 см на 5 локтей и размера 183 см на 4 локтя; видно, что 183 равны 6 футам, 8 полулоктям или 24 пальмам. Таким образом, полученное построение дает возможность вводить в интервалы между делениями Модулора дополнительные деления, соответствующие величинам исторических единиц измерения: дюйму, пальме, футу и локтю.
Эти дополнительные размерные величины могут быть использованы в строительной практике во второстепенных частях композиции для указания специфических размеров некоторых элементов строительных материалов [толщина каменных плит (в карьерах), ширины листового железа, размеры стандартизованных материалов: кирпича, черепицы, облицовочных материалов и т. д. ...]. Расхождение в 2,75 см для размеров, превышающих пять локтей, названное «добором», легко погашается за счет толщины швов, если число швов равно или больше 6, 8, 11, 18 и т. д. Серральта и Мезонье утверждают, что стены, высота которых определена по Модулору, могут быть с успехом расчленены самым разнообразным образом.
Мы видим, что Модулор удачно сочетается с прекрасными древними системами мер. Продолжая традиции, Модулор вносит в современное искусство что-то новое, плодотворное.
•
Еще ряд дополнительных построений, выполненных Мезонье, подтверждает возможность сосуществования Модулора и египетского локтя. Человеческая фигура с одинаковым успехом может быть вписана в кубы со сторонами, равными 226 см (по Модулору) или 22,875 см (египетский локоть), прекрасно при необходимости дополняющие друг друга. Дальше мы увидим, что объемная единица 226 х 226 х 226 будет с успехом применяться при проектировании квартир, и в особенности их внутреннего оборудования. Но не будем забегать вперед!
•
Ниже приведены высказывания горного инженера в отставке Крюссара (Париж).
1. Некоторые соображения по Модулору
Модулор может быть выражен геометрическим построением и системой числовых величин. Для полного его освоения следует овладеть обоими методами. Небольшая книга о Модулоре привлекает и, можно сказать, волнует именно тем, что ее автор запутался между этими методами; он их смешивает, производя впечатление человека, стремящегося сразу, одним взглядом, разглядеть и лицевую сторону ковра, и его изнанку, что ему, конечно, не удается. Лицевая сторона — это геометрия на основе интуиции и художественного чутья. Изнанка — это игра чисел. Часто ее признают занятием слишком рассудочным, не нуждающимся в творческом воображении; нет нужды говорить о том, что такое мнение в корне ошибочно; против него восстали бы и Пифагор и Платон.
•
Я убежден, что для полного понимания Модулора необходимы как геометрические построения, выполненные с помощью линейки и циркуля, так и числовые расчеты, при условии их обязательно раздельного выполнения. Геометрические построения следует делать так, как будто никаких чисел вообще и не существует, а расчеты — будто не существует никаких фигур, никакого пространства. Лишь после того как подобные исследования будут проведены, следует их сопоставить и обобщить. Не сомневаюсь, что только таким путем можно будет полностью разобраться.
Приведенные ниже замечания относятся лишь к числовым значениям Модулора и вовсе не касаются геометрии.
2. Исходные числовые величины
Основой Модулора, исходным числовым значением, на базе которого он построен, является число C = 1,618 (точно (√ 5/2) + ½). Возведенное в квадрат, оно дает 2,617924 или в четырехзначном выражении 2,618 — иначе говоря, то же число С, увеличенное на единицу. Возведя в квадрат (√ 5/2) + ½) мы получим эту же величину, увеличенную на единицу.
Арифметика не знает другого положительного числа, обладающего таким свойством. На основе Модулора лежит именно это свойство числа С. Оно и является основой всей сетки.
3. Сетка С.
| Возьмем три величины: | 1 | С | С • С (1) |
| выраженные в числах, они равны | 1 | 1,618 | 2,618 |
причем третье число равно сумме двух предыдущих. Для развития сетки установим четвертое число ряда — С • С • С. Оно, по-видимому, может быть получено умножением всех трех чисел ряда (1) на величину С:
| С | С • С | С • С • С |
| 1,618 | 2,618 | 4,236 |
причем последнее, разумеется, будет равно сумме двух предыдущих.
Сетка Модулора может получить дальнейшее и вполне очевидное развитие:
1) исходная позиция........ 1
2) основная числовая величина........ 1,618
3) сумма 1) и 2)........ 2,618
4) сумма 2) и 3)........ 4,236
5) сумма 3) и 4)........ 6,854
6) сумма 4) и 5)........ 11,090
и так далее до бесконечности. Это и есть красный ряд Модулора.
4. Основа
В любой сетке или ткани, помимо утка, должна быть и основа. Модулор определяет ее путем удваивания предыдущих цифр. Естественно, что новый синий ряд будет обладать теми же свойствами, что и красный. Каждое число ряда равно сумме двух предыдущих чисел:
1') исходная позиция........ 2
2') основная числовая величина 2 • 1,618........ 3,236
3') сумма 1') и 2')........ 5,236
4') сумма 2') и 3')........ 8,472
5') сумма 3') и 4')........ 13,708
б1) сумма 4') и 5')........ 22,180
и так далее до бесконечности.
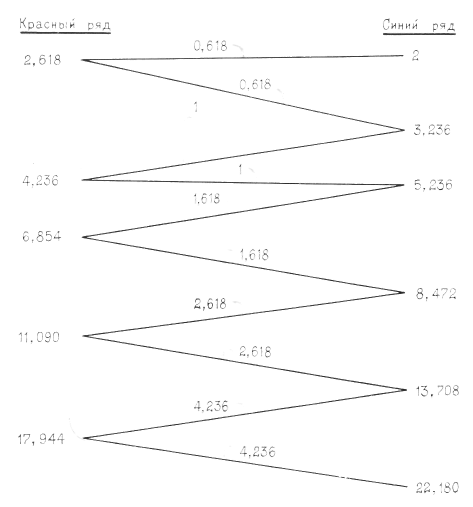 |
5. Перекрестное переплетение сеток
Остается посмотреть, как переплетены уток и основа сетки Модулора. Переплетение вполне удовлетворительное, так как в возрастающем ряде чисел последовательно повторяются числа обоих рядов (см. схему).
Отбросим на время первые члены ряда, представляющие собой как бы кромку сетки; но об этом несколько ниже.
Мы видим, что имеется абсолютно правильное чередование чисел красного, синего, красного рядов. Отметим, что величины интервалов между числовыми значениями показаны числами на наклонных прямых. Эти числа обладают интересными свойствами:
1. Каждый член красного ряда определяет точную середину между двумя смежными членами синего ряда, из которых один меньше, другой больше его;
2. Интервал между членом красного ряда и двумя смежными членами синего ряда постоянно увеличивается в соответствии с числами ряда 1 — 1,618 — 2,618 — 4,236 и т. д....
В этих свойствах нет ничего загадочного; их легко объяснить: это — прямое следствие свойств, присущих числу С (помноженному на 2).
6. Изменение направления сетки
Возвратимся к исходной позиции в ряде чисел от 1 до С, равного 1,618. Вместо того, чтобы идти слева направо и образовать числа путем их сложения: 1 — С = 2,618, мы можем пойти влево, образуя числа, которые в сумме с единицей будут равны С; таким будет, очевидно, С — 1 = 0,618. Отсюда получаем три числа ряда:
С—1 ..... 1 ..... С
Соответствующие
0,618 ..... 1 ..... 1,618
Принимая во внимание известные нам свойства числа С, можно рассчитывать на то, что, умножая первый член на С, мы получим второй. И действительно, 0,618 • 1,618 = 0,999924 или практически 1 (поскольку, строго говоря)
0,618 = (√ 5/2) + ½).
Таким образом, образуется новый числовой ряд, идущий справа налево, при котором каждый новый член (слева) представляет собой разницу двух предыдущих. Новая сетка чисел будет иметь следующий вид:
1) исходная позиция..... 1
2) основная числовая единица..... 0,618
3) разница между 1) и 2)..... 0,382
4) разница между 2) и 3)..... 0,236
5) разница между 3) и 4)..... 0,146
6) разница между 4) и 5)..... 0,090
7) разница между 5) п 6)..... 0,056
и так далее до бесконечности.
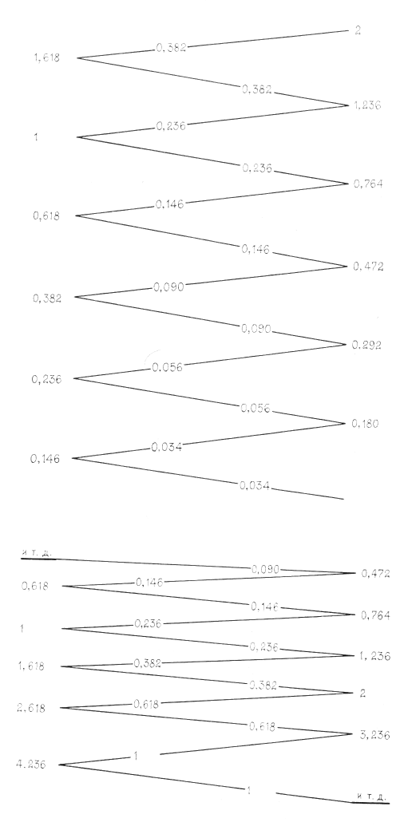
7. Изменение направлений основы при перекрестном переплетении сеток
Числовые величины синего ряда являются удвоенными числами красного ряда; перекрестное переплетение сохранено.
Сохранились свойства, приведенные выше (см. схему).
 |
8. Сочетание возрастающего и убывающего рядов
Теперь стало ясным, как сочетаются крайние показатели сеток (ограничимся только числовыми величинами, близкими к краевым показателям): Сопряжение числовых величин безупречно. Все закономерности сохраняются от начала до конца; не осталось и следа от той «кромки», от которой мы повели счет вправо и влево.
Таковы основы «теории Модулора в ее арифметическом выражении».
При желании увидеть «изнанку ковра» лучшего нечего и искать.
Пусть и математик и художник изучают его лицевую сторону.
Полное понимание Модулора достигается сразу при обобщении обеих сторон.
P. S. Для того чтобы не запутать все на свете, я выделил в постскриптум частный вопрос, который можно было бы назвать отношением между сеткой и основой.
Для этого рассмотрим последовательные числа красного ряда, примыкающие к сопряжению убывающих и возрастающих чисел ряда
| 1C | 2C | 3C | 4C |
| 2 — С | С— 1 | 1 | C |
| 0,382 | 0,618 | 1 | 1,618 |
Каждое число, естественно, является суммой двух предыдущих; кроме того, сумма крайних чисел (1С и 4С) равна 2, т. е. удвоенному 3С, т. е. началу синего ряда. Следовательно, из одних лишь членов красного ряда можно образовать синий ряд путем сложения двух несмежных членов ряда, отказавшись, иначе говоря, от основного правила, изложенного в параграфе 3. Это равносильно тому, чтобы при изготовлении сетки пропускать промежуточные нити. На этих чисто числовых примерах можно проследить основы, на которых построены два смежных квадрата.
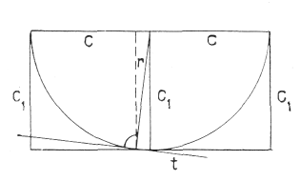
Взяв за основу квадрат, мы трижды повторяем хорошо известное построение деления в отношении золотого сечения. Сумма сторон верхнего и основного квадратов равна удвоенной стороне среднего квадрата. Это важное свойство очевидно из приведенного чертежа (рис. 7).
Все попытки более упрощенных построений (построение Палладио, решение Майяр) дают лишь приближенные результаты.
Выраженное в числах построение Палладио (√ 5/2) + ½) + (√2 — 1) = 2,032 свидетельствует об ошибке в 1,6%;
Решение Майяр отвечает выражению (√ 5/2) + (2/√5) = 0,9√5 = 2,0124 с ошибкой в 0,6 % . Оно в 2,5 раза точнее построения Палладио. Однако единственно правильным является построение, показанное на рис. 7.
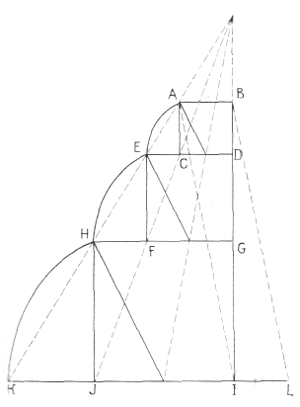 |
АВСD — исходный квадрат. Пользуясь классическим построением, находим квадрат DEFG и GHJI, затем положение точки K.
Переносим величину АВ в IL, проведя линию AI и параллельную ей BL. Очевидно, что KL= 2 GH. Если начинать построение с GH, необходимо:
1) определить DE, а затем и АВ, ведя построение в обратном порядке;
2) затем найти KL уже обычным путем.
Суммирование KI и АВ дает искомое решение.
•
Из письма Жана Дейра (АСКОРАЛ), Государственное управление по экономике.
«Париж, 31 августа 1950 г.
... Я попытался вдуматься в перспективы, которые вы раскрываете в книге «Модулор», 1948 г., говоря о выработке всеобщей гармонической системы мер. Мне хотелось бы поделиться с вами четырьмя своими соображениями:
1. На основе Модулора Вы сможете разработать логарифмическую систему мер.
2. Эта система позволила бы упростить числовые выражения больших и малых величин.
3. Вы сможете использовать свойства логарифмов для упрощенных подсчетов площадей и объемов.
4. Необходимо, однако, проверять пределы применения аддитивных свойств этой системы.
1. Возможность создания логарифмической системы мер на основе Модулора
Отношение Ø = (1+√5) / 2 = 1,6178 ≈ 1,62
в качестве основы ряда Фибоначчи можно принять для построения новой логарифмической системы, которая сможет конкурировать с натуральной и десятичной системой логарифмов.
Назовем их, с вашего разрешения, золотыми логарифмами (на основе золотого сечения) или, еще проще логор. (S)*.
*От logarithme aural золотой логарифм. (Прим, ред.)
Золотой логарифм числа N равен:
Фx = N или 1,6178х = N. Следовательно, логор. 1,62° или логор. 1/=0
логор. 1,62 = 1;
логор. 1,62кв = 2 и т. д.
Для того чтобы придерживаться человеческого масштаба, вы принимаете вспомогательную дополнительную величину — 1,83 м, соответствующую росту атлета в 6 фунтов.
Назовем эту единицу мегалантропом, или сокращенно меганом (1 меган = 1,83 м).
Получаем приведенную ниже переводную таблицу метрических мер, которую можно в случае необходимости экстраполировать. Переведем в логоры.
В качестве логарифмической единицы принимаем золотой логарифм от Ø меган = 1,62 меган. Назовем эту единицу альмеган (от алгоритма). Приводим переводную таблицу:
2,96 метра = 1,62 мегана = 1 альмеган;
0,70 » = 0,37 » = 2 »;
3,66 » = 2 » = 1,45 ».
(для красного ряда получаем дробные альмеганы).
2. Размерные величины, выраженные в альмеганах (как все логарифмические величины), удобны для выражения очень малых и очень крупных величин
Они определяют необходимое число градаций (восходящих и убывающих) основного красного ряда, отделяющих исходную точку, соответствующую росту мегалантропа, от искомой величины. Примеры (не считаясь с возможностью ошибок в расчетах):
1. Расстояние от Парижа до Марселя
800 000 м = 800000 меганов / 1,83 = около 28 альмеганов.
2. Диаметр капли воды
5 мм = 0,005 меганов / 1,83 = около 13 альмеганов.
3. Диаметр Млечного пути
5000 световых лет = 10 в 21 метров = 10 в 21 меганов / 1,83 = около 100 альмеганов.
4. Длина световой волны в пустоте
0,0006 мм = 6 метров / 10 в 7 = 6 / 1,83 x 10 в 7 альмеганов = около 31 альмеганов.
Таким образом, все самые крупные и самые мелкие; величины, выраженные в альмеганах, дают числовые величины, отвечающие человеческому масштабу. Очевидно, что приняв в качестве исходной единицы длины метр, мы обнаружили бы такую закономерность. Каким бы размерностям не отвечали принятые величины, количество метров, выраженное в логарифмах, будет отвечать человеческому масштаб). В диапазоне между числовыми значениями длины звуковых волн и диаметра Млечного пути на шкале Модулора размещается всего 131 деление.
3. Использование свойств Модулора для исчисления площадей и объемов
Речь идет о простом использовании свойств логарифмов.
Для примера приведем подсчет площади комнате в квадратных метрах и в квадратных меганах:
1 квадратный меган =1,832=3,35 м2.
Размеры комнаты: 4,79Х 7,74 м или 2,62 X 4,24 меганов
Арифметический подсчет определяет площадь комнаты в 37 м2 или 11 кв. меганов.
Используем золотые логарифмы или логоры:
логор. 2,62 мегана = 2 альмегана;
логор. 4,2 мегана = 3 альмегана.
Логор. площади, выраженный в квадратных меганах составит 2 + 3 = 5.
Экстраполируя переводную таблицу, получаем:
11 кв. меганов или 11 X 3,35 = 37 м2, что подтверждает результат арифметического подсчета.
Подробная переводная таблица позволила бы быстро производить определение величин дробных альмеганов.
4. Распространение аддитивных свойств Модулора
Здесь пойдет речь о самых серьезных трудностях при использовании Модулора в качестве всеобщей системы мер.
Основным свойством любой системы мер является возможность производить сложение размерных величин.
Логарифмические системы, как правило, таким свойством не обладают.
Этим я хочу сказать, что логарифм суммы двух чисел не может быть непосредственно определен по логарифмам этих чисел. Так, например, по десятичной системе:
log 10 = 1;
log 1000 = 3.
Вместе с тем
log (1000 + 10) = log 1010 = 3,0043.
Этот итог мы определяем по таблице логарифмов. Прямой связи между log 1010 (3,0043), log 10 (1) и log 1000 (3) нет.
В то же время система золотых логарифмов обладает рядом аддитивных свойств, поскольку у ряда чисел существует прямая связь между логарифмами этих чисел и логарифмом их суммы.
Таковы основные свойства Модулора, относящегося к ряду Фибоначчи:
Ø + Ø в n+1 = Ø в n+2
Таким образом, рассматривая три последовательных члена красного ряда, мы видим, что золотой логарифм третьего члена (являющегося суммой двух предыдущих) находится в простой связи с золотыми логарифмами двух первых членов.
Если n — это золотой логарифм первого, n + 1 — логарифм второго, то золотой логарифм суммы равен n + 2.
Таким образом мы можем суммировать некоторые величины, используя свойства золотых логарифмов. В этом и заключается основная трудность, ибо сказанное вовсе не означает, что эти свойства Модулора распространяются на все величины.
Так, например, взяв два каких-либо случайно выбранных числа, золотые логарифмы которых равны (1,83 и 2,67), определить логарифмы их суммы на основе величин 1,83 и 2,67, очевидно, нельзя. Если бы удалось доказать такую возможность, то Модулор одержал бы полную победу и мог бы стать всеобщей гармонической системой не только по существу, но и на практике.
Вопрос этот весьма важен, и, по-моему, им должны заняться математики.
Как бы то ни было, Ваше открытие замечательно. Вне зависимости от того, свойственна ли ему полная или только частичная аддитивность, Модулор является инструментом, которого недоставало тем, кто занимается стандартизацией, способной гармонично сочетать точность и строгость с художественными качествами.
Жан Дейр»
•
Письмо доктора математики Андреаса Шпейзера
«Базель, 13 июня 1954 г.
Дорогой друг, спасибо за Ваше письмо и особенно за замечательную книгу о Модулоре. Я прочитал ее с великим удовольствием и воспринял как знак уважения художника, увлеченного математикой. Вы оказались в отличной компании, поскольку все великие художники находились под чарами чисел. В своем письме Вы спрашиваете: правда ли, что можно прибегать одновременно к помощи и геометрии и чисел? Отвечаю:
Мы располагаем двумя возможностями познания внешнего мира:
1. Числа. С их помощью мы «познаем внешний мир», т. е. существование множества других людей, порядок, пропорции, красоту и т. д.
2. Пространство. В нем мы наблюдаем множество неодушевленных предметов, лишенных жизни, красоты, но «занимающих место» (лежащих, стоящих, распростертых и т. д...).
Теперь о Модулоре. Вы, конечно знаете, что Лука Пачиоли написал замечательный трактат, посвященный божественной пропорции. В нем он говорит о 13 чудесных свойствах золотого сечения. Он дал каждому из них пышное наименование и поведал нам о радостях, доставленных ими Леонардо да Винчи. Ваша заслуга заключается в том, что Вы открыли четырнадцатое свойство.
Вы построили два ряда Фибоначчи, из которых второй является удвоением первого, и выявили закономерность в свойствах четырех последовательных чисел такого ряда. Взяв, например, числа 5, 8, 13, 21, видим, что сумма первого и последнего чисел, т. е. 5 + 21, равна удвоенному третьему числу; 5+21=26. В то же время разница между четвертым и первым числами равна удвоенному второму 21 — 5 = 16 = 2 • 8.
Хочу представить эту закономерность в общем виде, понятном для любого школьника. Обозначим буквами a, b, с, d четыре последовательных числа, причем c = a+b и d = а + 2b, откуда a + d = 2a + 2b = 2c и, наконец, d — 2b.
Этим и объясняется связь между вашими красным и синим рядами.
Письмо Жана Дейра также справедливо, но должен сказать, что сейчас уже не пользуются логарифмами. Теперь все расчеты делают на счетных машинах (во много раз скорее и точнее). Я понимаю, что Вы стремились иметь систему мер, легко применяемую в архитектуре, и что вам необходимы целые числа для достижения гармонии. Мне поэтому представляется, что ваша система мер действительно приемлема для художников. В конечном же счете, когда дело дойдет до рабочего, придется давать ему все размеры в метрах, что, кстати, не представит никаких трудностей. Для этого необходимо лишь перемножить ваши числа на вашу же единицу, выраженную в метрах. Что касается межпланетных расстояний, то к пим я отношусь скептически. В течение многих столетий пытаются установить эти закономерности, этим занимались в свое время Кеплер и Тициус, определившие некоторые из них; в настоящее время этими вопросами настойчиво занимается профессор Вейцзеккер в Геттингене. Я не слишком верю в то, что эта загадка может быть решена с помощью золотого сечения. Примите, дорогой друг, заверения в моих лучших чувствах.
А. Шпейзер».
 |
•
Наша дискуссия велась на высоком научном уровне, на весьма высоком.
Однако слово за теми, кто пользовался Модулором... Ведь мелочей вообще не существует — ни в живописи, ни в архитектуре, ни в жизни! Альфред Нейман признает значение отношения Ø. Любитель всяких расчетных таблиц, цифр, числовых подобий и сочетаний, он составил множество таблиц на основе отношения Ø.
Эти таблицы позволили установить ряд числовых величин. Так, например, 0,462 м близко к величине аттического локтя, равного 0,46 м; с помощью отношения золотого сечения локоть переводится в метрическую систему, чем и объясняется происхождение в Парфеноне точных метрических размеров, высота колонн которого равна 10 м. Это было установлено мною. Египетский (царский) локоть, равный 0,524, по таблице Неймана равен 0,5236 м (рис. 8).
Далее Нейман пишет: «Для того чтобы создать правильную систему мер и пропорционирования, необходимо объединить «геометрическую» единицу мер с «антропометрической». Метр пока еще является основой научных измерений и, следовательно, технической цивилизации. Любопытно, что метр одновременно является «антропометрической» мерой. Я установил, что должна существовать общность между метром, являющимся земной мерой длины, и человеческими размерами. Многие критикуют использование метра в качестве основы системы мер, поскольку считают его не антропометрической мерой, а научной абстракцией. Подобное мнение необоснованно. Метр представляет собой обновленную форму старых человеческих размеров. Метр — это удвоенный локоть, который лишь впоследствии был разделен на три фута, до настоящего времени являющегося единицей английской системы мер»... (Ярд = 3 футам).
Самой древней единицей длины, известной сегодня. является двойной локоть вавилонского царя Гудеа; она была установлена в 22 веке до н. э. и равна 990— 996 мм, т. е. примерно метру.
Связь между мерами времени и пространства была известна во времена древних цивилизаций. Меры веса прошлого соответствовали примерно килограмму. В древней Греции при назначении диаметра колонн часто применяли модуль, близкий к метру, например, в Тезейоне в Афинах 1,004 м, в Эгинском храме 1,01 м...
В наше время английский Институт стандартов утвердил величину модуля в 101,6 мм; в Америке модуль установлен в 10,16 см.
Отсюда Нейман делает вывод: «Сказанное нами подтверждает обязательную необходимость объединения десятичной системы m с отношением золотого сечения «Ф». Эту систему можно назвать «mФ» — система «Эм-фи»...»
Чудесно, я приветствую такое трогательное согласие и даже еще более тесный союз. Обращаю, однако, внимание на камень преткновения — американский модуль равен 10,16 см. Эта величина имеется в красном ряду: 10,2. Но между построением всего человеческого окружения на бесконечном сложении 10 см (или 10,16) и построением на основе Модулора — целая пропасть.
Нейман признает Модулор заслуживающим внимания, несмотря на то, что он основан на «произвольном» росте (в этом он прав!) человека в 1 м 83 см; он в восторге от того, что ему удалось установить, что в таблицу величин mФ входят ряды Модулора с незначительными отклонениями; в этом он видит подтверждение того, что «Ле Корбюзье не лишен интуиции».
Инженер-механик из Лилля выразил пожелание увязать Модулор с «рядами Ренара», используемыми в механике. Вот письмо, адресованное им моему заместителю Воженскому, являющееся откликом на доклад, сделанный последним в Лилле.
«5 июля 1951 года
Мсье, сожалею, что не смог присутствовать на докладе, сделанном Вами 18 января в Лилле. Я познакомился с ним по тексту и был поражен изображением под наименованием Модулор.
Вы можете сказать, что замечания, сделанные механиком, неприемлемы для архитектора. Но почему бы вам не принять вместо точного значения отношения золотого сечения
1,618 = 1 / 0,618
близкую к этому величину ряда Ренара
1,585 = 5√10.
Относительная ошибка, определяемая разницей между 1,618 и 1,585, равна 2%. Разве это существенно с точки зрения гармоничных пропорций? Ряды приобретают следующий вид:
 |
(десятичные знаки значения не имеют: можно поэтому ограничиться второй строчкой). Рост человека определится в 1,80 м, высота стула в 0,45, стола в 0,71, двери в 2,20, низкого кресла в 0,36 м, размер кирпича 11 х 22 см.., облицовочной плитки 11 см...
В красном и синем рядах по 10 двух- и трехзначных чисел, что точно соответствует ряду Ренара R — 20, на котором основана стандартизация в машиностроении.
Не облегчит ли это работу, учитывая, что архитекторы используют в строительстве материалы заводского изготовления? Когда в своем докладе Вы сравнивали размеры Модулора с футами и дюймами наших английских друзей, я подумал о возможности еще большего механического упрощения путем дополнения ряда R — 10 десятью промежуточными числами:
 |
тогда как размерные величины обоих рядов Модулора не являются простыми, кратными футу и дюйму. Однако в этом ряду имеется резкий скачок от 1,60 к 2,00 с пропуском величин, отвечающих человеческому росту. Поэтому от него следует отказаться. Чтобы вы подумали, если таблицу Модулора заменить следующей:
 |
Чтобы легче было запомнить таблицу, мы исходим из роста человека 1,800 мм, а затем множим или делим эту величину на 2, условно сохраняя лишь первые два знака:
 |
Вы сопоставляете с музыкальной гаммой: это сопоставление может быть уточнено, поскольку интервалы между
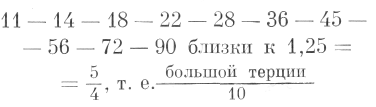 |
или к большой терции по темперированному строю 1,2589 = 10√10
Возможно, что я ломлюсь в открытую дверь — но был бы счастлив узнать, почему (как мне кажется) вы пренебрегаете этой дверью.
А. Мартино-Лагард»
Подобные предложения — округлить числовые значения Модулора и привести их в соответствие с другими рядами — уже делались. Я считаю, что Модулор является орудием, придающим уверенность при замысле и его разработке... То, что верно сегодня, останется верным и через шесть месяцев, через шесть лет и через шесть дней, выполнено ли оно на чертежах одного и того же или разных проектировщиков в разных мастерских любых стран.
Интервалы между значениями Модулора дают возможность нюансировать размеры по желанию, подобно тому как «вибрато» при игре на скрипке дополняет тон более высокими и низкими тонами, обеспечивая восприятие верного тона. Конечно, здесь есть о чем подумать, поэтому читатели могут с этим соглашаться или не соглашаться и поспорить с пользой для дела.
•
Игра с числами может завести далеко. Вот краткое письмо, направленное Лабарту по вопросу об исследованиях космоса (осталось без ответа).
«Париж, 5 июня 1956 г.
Два месяца назад я направил редакции вашего журнала «Constellation» («Созвездие») свою книгу «Модулор».
Наше тревожное время, конечно, не слишком располагает к подобного рода занятиям.
За восемь лет со времени его изобретения в 1948 г. я ни разу не пытался поднять шум вокруг Модулора. Но ваши исследования космоса, поразившие всех в фильме Николя Ведреса, взволновали меня, и вот почему.
Между 15 / 1000 (пятнадцати тысячных) миллиметра и окружностью земли в Модулоре предусмотрено (примерно) 270 интервалов. Следовательно, порядковые числа в ряду:
№ 1 = 15 тысячных миллиметра;
№ 270 = 40000 километров,
а № 300 будет уже величиной космической.
На основе этих данных уже можно составлять расписания, высчитывать время, решать вопросы снабжения и т. д., и т. д. Расстояние Земля—Луна равно (примерно) числу № 285 Модулора (a) ~ + № 41 (b) + № 9 (c)
Это значит, что число № 285 определяет колоссальные расстояния.
Число № 41 соответствует порядку расстояний от метра до километра; число № 9 — приводит нас к величинам микроскопическим (приведенная здесь нумерация чисел ряда произвольна). Их можно было бы записать:
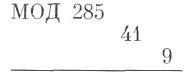 |
МОД 285. 41. 9., что дает возможность произвести точные расчеты.
Об этом я уже думал раньше, но сейчас впервые применил индекс МОД. Надо будет еще подумать.
Модулор охватывает размерные величины от бесконечно малых до бесконечно больших. Это во всех своих значениях возвратный ряд.
Со временем можно будет записывать размеры следующим образом МОД 47,3 и т. д., и т. д. .. , упразднить футы, дюймы и метры, распространив на весь мир десятичную систему мер.
Исследования и создание Модулора не ставили себе целей столь космического масштаба».
•
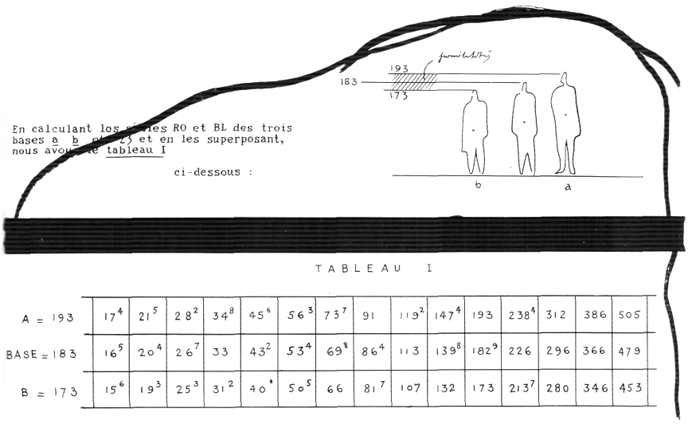
Завершая этот раздел, скажу еще об одном виде интервалов. О них мне сообщил парижский архитектор М. Ротье, утверждающий, что такие интервалы весьма пригодны при определении модульных размеров площадей и объемов в жилищном строительстве. Как архитектор, он учитывает разницу в толщине материалов, в росте людей высотой 1,73, 1,83 и 1,93 м. что приводит его к введению промежуточных делений, членящих интервалы шкалы Модулора пополам. Эти соображения архитектора-практика вполне справедливы. В этом вопросе положение такое же, как в вопросе использования графических методов построения в живописи, где сначала следует определить, какая часть картины должна быть откорректирована этим методом. И в архитектуре следует установить, какие конструктивные элементы подлежат корректировке методом графического построения или, по обстоятельствам, с учетом градаций Модулора.
Задача заключается в том, чтобы учитывать то, что мы видим. Длины, площади и объемы мы воспринимаем зрением, и необходимо их тонко пропорционировать. Чему же надо уделить основное внимание? Пространству комнаты или толщине перегородки?
Какие размеры окон наиболее важны: размеры стекол или всего оконного проема? Это и следует установить в каждом отдельном случае.
 |
•
Итак: будем внимательно смотреть вокруг себя, измерять, пусть появится интерес к пропорционированию; это не дается сразу. Приходится признаться в горькой истине, что строим мы стихийно, не считаясь с системой хорошо взвешенных и согласованных пропорций. Инженеры сделали шаг вперед в этом направлении, руководствуясь в стандартизации требованиями экономичности. Стремясь перебросить мосты через моря и океаны и считаясь с тем, что предметы промышленного производства должны применяться повсеместно, они разработали стандарты. Их стандартизация характеризуется известным упрощенчеством и не обеспечивает полной творческой свободы. Однако прогресс человечества и устанавливаемые правила не должны исключать или хотя бы ограничивать творческое воображение. Мы стали с открытыми глазами смотреть вокруг себя и изучать свое жилище.
Часто, изучая жилище прошлого, созданное некогда каменщиками, столярами, штукатурами, мы находим ответы на возникающие вопросы: это объясняется цеховыми правилами, передаваемыми от поколения к поколению; они, однако, накапливаются, искажаются и со временем насыщаются всякими таинственными секретами. Вся эта премудрость доходит до нас в упрощенном и чисто «прикладном» виде.
Время от времени (и это имеет отражение и в полученных нами письмах) появляются глашатаи, превозносящие теории тысячелетней давности. Естественно, что эти теории не отвечают и не связаны с очевидными запросами современности. Такие глашатаи упиваются собой и намекают на свою ученость и осведомленность. Иногда ... они начинают «священнодействовать» и вещать на таинственном языке. Нам сообщают, что произведения 8 на 108 = 864: что 108 и 7 означают число 108 и святой дух; и что 216 это удвоенное 108 ...
Лично меня они сейчас, когда я занимаюсь исследованиями в области чисел, несколько занимают: но я хорошо знаю, что дважды 54 = 108; восемь раз 108 = 864 и т. д.
Я считал всегда и считаю, что размерная величина 108 сантиметров совершенно не равнозначна числу 108, смысл и назначение которого мне неизвестны. Если я перевожу 108 см в футы, то получаю 26 дюймов и число 26 перестает быть священным числом, восходящим к числу 108, и т. д.... Число 108 в 1945 году послужило мне основой первого Модулора, построенного на росте человека в 1 м 75 см. Совпадение чисел ни о чем еще не говорит. Знаю, что существует метафизика, связанная с тысячами символов, которым приписывается тысяча и одно значение. Но я-то ведь только строитель. Считаю необходимым еще раз настоятельно подтвердить важное значение мысли:
«Модулор является орудием, придающим уверенность при принятии решений. То, что сегодня верно, будет верным и через шесть месяцев, через шесть лет и через шесть дней, в чертежах одного и того же или разных проектировщиков в разных мастерских любых стран».
Что верно, то верно! Мы имеем дело со сферой чисел. Вы хотите «округлять» и согласны на компромиссы? Во имя кого? Во имя чего? Единственный путь к решению — это правда.



Добавить комментарий